그래프(Graph)
그래프(Graph)
- 현실 세계의 사물이나 추상적인 개념간의 연결관계를 표현한 것
- 일반적이고 강력한 자료구조
- 정점(Node or Vertex)과 간선(Edge or Branch)으로 구성
- G=(V,E)로 표현가능 , V: 정점집합 / E: 간선집합
주요 용어 정리
경로 Path
- 끝과 끝이 서로 연결된 간선들을 순서대로 나열한 것
- 단순경로: 경로 중 한 정점을 최대 한번만 지나는 경로 의미(일반적)
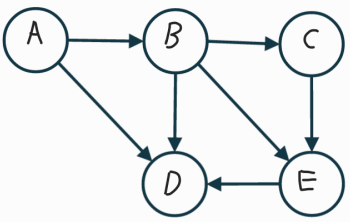
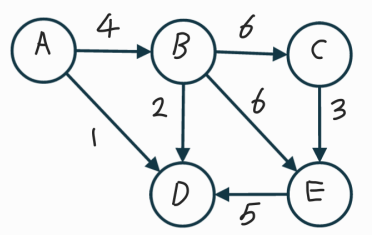
ex) A –> E로 가는 경로
A –> B –> E
A –> B –> C –> E
A –> B –> D –> E
사이클 cycle
- 시작한 점에서 끝나는 경로
- a.k.a. ‘회로’
- 단순 사이클: 같은 정점을 두 번 이상 방문하지 않는 사이클 (일반적 / 시작점 제외)
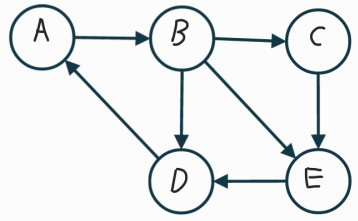
ex)단순 사이클
A –> B –> D –> A
A –> B –> E –> D –> A
A –> B –> C –> E –> D –> A
…
방향그래프 Directed Graph
- 간선에 방향성이 있는 그래프
- ‘비대칭적’: 주로 방향 그래프 사용
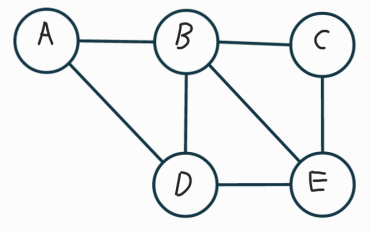
무방향그래프 unDirected Graph
- 간선에 방향성이 없는 그래프
- a.k.a. ‘양방향 그래프(Bidirection)’ :A-C = A->C && A<-C
- ‘대칭적’: 주로 무방향 그래프 사용
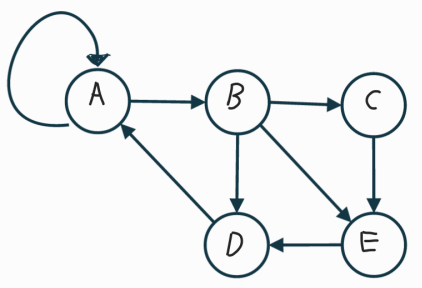
루프 Loop
- A->A와 같이 사이클을 이루는 것
가중치 weight
- 간선에 주어진 값
- A->C로의 시간, 비용, 거리 등…
차수 Degree
- ‘분지수’
- 정점과 연결되어 있는 간선의 개수
- 인접한 정점이나 edge의 개수
- 내향분지수(indegree): 들어오는 간선 수
- 외향분지수(outdegree): 나가는 간선 수
ex) B의 차수
: B’s degree = 4
: B’s indegree = 1
: B’s outdegree = 3
인접 adjacent / incident
-
- Adjacent
- u, v 정점의 인접
-
- Incident
- 정점 u에 간선 e(u, v) 인접 (부속)
연결 성분 connected component
-
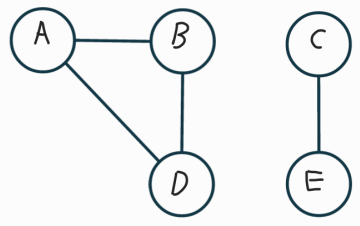
- 연결 성분
- 연결된 한 덩어리
여러가지 그래프
-
- 완전 그래프 Complete Graph
- 모든 정점이 edge로 연결되어 있을 경우
; n개의 정점과 n*(n-1)/2 개의 엣지
-
- 단순 그래프 Simple Graph
- 둘 사이가 이진관계
-
- 다중 그래프 Multi Graph
- 같은 간선이 중복됨
-
- 부분 그래프 Subgraph
- 원래 그래프의 일부, 엣지 노출x
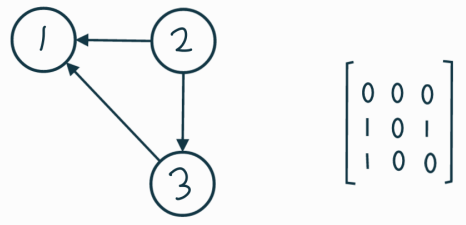
인접행렬 adjacency metrix
- 정점의 개수를 n개라고 했을 때
n*n 개수를 표현하는 이차원 배열을 생성 - adj[a] [b] = 0 or 1 or 가중치 값 ( 간선 유무 or 가중치 )
-
공간복잡도 O( n ^2)
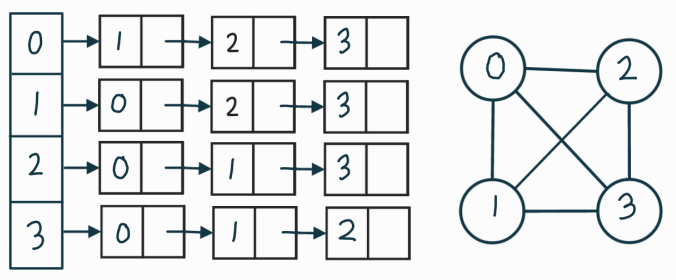
인접리스트 adjacency list
- 원래 연결리스트를 이용해서 구현
- 보다 쉬운 구현 => vector와 같은 동적배열 이용
- 헤드노드를 배열로 묶음 & 인접한 애들을 list로
=> 정점에 바로 접근하도록
- 공간복잡도 O(V+E) , V는 정점개수, E는 간선개수
- 무방향: 양쪽 둘 다로 가는 방향 엣지 추가시 리스트로 표현 가능
- 따라서 같은 표현이라 인접리스트만 가지고 무방향인지 방향인지 확정할 수x
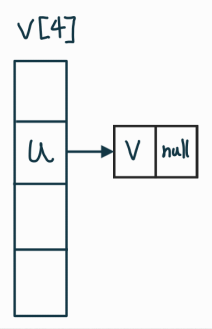
인접리스트 코드
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
vector<vector<<int>> v(4);
int main(){
int n, m;
cin >> n >> m;
for (int i=0; i < m; i++){
int u,v;
cin>>u>>v;
v[u].push_back(v);
}
}

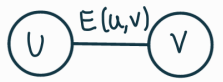
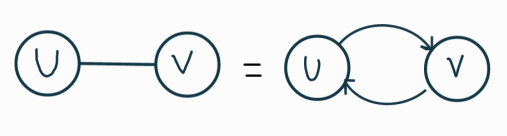
Comments