Hong

끄적끄적

3. 탐욕적 기법(Greedy Algorithm)

탐욕적 기법(Greedy Algorithm)은 이름 그대로 항상 눈앞의 가장 큰 이익만을 좇는 방법입니다.

어떤 경우에 사용할까?

그리디 알고리즘으로 최적의 해를 구할 수 있는 문제는 많지는 않다. 하지만 이런 방법이 통하는 문제들이 분명 존재하고 전략을 파악했을 때 간단히 해결이 가능한 문제가 많기 때문에 대회나 코테에 자주 나온다.

  1. 문제를 해결하는 과정에서 한 가지의 전략을 선택을 하였을 때 그 이후에도 원래 문제와 동일한 성질이 성립하여야 한다. 성질이 동일하게 보존되어야 썼던 전략을 계속 취해도 답을 구할 수 있기 때문이다.
  2. 보통 풀이가 가장 큰, 긴, 빠른~ 것부터 해결해야 하는 경우가 많은 편이다 보니 정렬이 필요할 때가 많다.

예시

그리디 알고리즘의 대표적인 예시로 동전 문제가 있다. 백준 문제를 통해 알아보자.

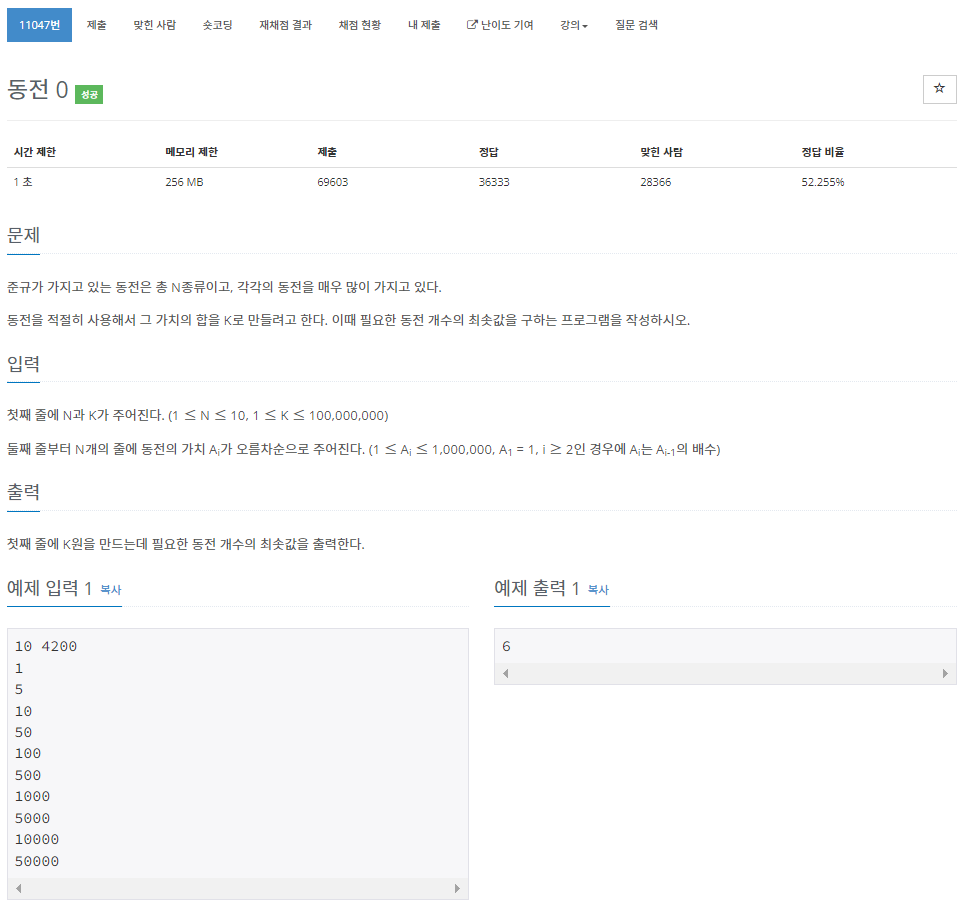
BOJ 11047 BOJ11047

요약

N 개의 종류의 동전이 있고 각 동전은 무수히 많다. 동전을 조합해서 가치의 합을 K로 만들려고 할 때 필요한 동전의 최소 개수를 구하는 문제이다.

풀이

첫 번째 예제 입력값을 보자 1, 5, 10, 50, 100, 500, 1000, 5000, 10000, 50000의 가치를 가진 동전들로 4200원을 만들어야 한다.

이 문제의 풀이법은 생각보다 쉽게 떠올릴 수 있을 것이다. 무조건 사용할 수 있는 범위 내에서 가장 큰 가치를 가진 동전을 많이 사용하는 것이다. 4200원을 만들기 위해서 4200원 이하의 가장 큰 액수가 1000원이므로 4번 사용해서 4000원을 만들 수 있다. 그러면 200원이 남게 되고 그다음으론 100원짜리를 두 번 써서 총 1000 x 4 + 100 x 2로 4200원을 만들 수 있고 답은 6이 된다.

그리디가 성립하는 이유

왜 이런 풀이법이 성립할까? 이 문제의 입력 조건을 확인해 보면 오름차순으로 입력되는 동전이 가치가 돈값의 배수이다. 따라서 큰 금액의 동전은 무조건 작은 동전 여러 개로 교체할 수 있을 수 있게 되고 반대로 작은 동전 여러 개를 큰 동전 하나로 바꿀 수 있다면 동전의 개수를 줄일 수 있게 된다.

저 배수의 성질이 성립하지 않는 경우를 예시를 들어보면 10, 50, 60원의 동전을 사용해서 220원을 만든다 가정해 보자. 가장 큰 60원을 사용하므로 60 x 3을 해서 180원까지 사용하게 되고 40원이 남게 되고 다음으로 사용할 수 있는 가장 큰 동전은 10원이므로 10 x 4 + 60 x 3으로 7개의 동전을 사용하게 된다. 하지만 50 x 4 + 10 x 2로 6개의 동전을 사용하는 게 가능하다.

저 배수라는 성질이 있기에 위에서 얘기했던 사용할 수 있는 가장 큰 동전을 우선적으로 사용하자는 전략을 사용하여도 동일한 성질이 지속되어서 끝까지 같은 전략을 사용할 수 있다.

정리

보다시피 생각보다 쉽지 않은 알고리즘이다. 위의 동전 문제는 비교적 쉬울지 모르지만 대부분의 문제가 딱 보고 그리디를 떠올리기 힘들 때가 많다. 읽어보다가 갑자가 그리디일 거 같은데? 하는 느낌이 올 때가 있다. 반례가 있을 가능성이 높으니 생각을 많이 해봐야 한다.

관련 문제

Comments

You May Also Enjoy