Hong

끄적끄적

4. 분할정복(Divide and Conquer)

분할정복 알고리즘은 말 그대로 분할하고 정복하는 알고리즘이다. 먼저 문제를 나눌 수 없을 때까지 나누어 각각을 풀고 다시 합병하여 문제의 답을 얻는다.

어떻게 푸는가?

  1. Divide : 문제가 분할이 가능한 경우 두 개 이상의 문제로 나눈다. (가장 중요!!!)
  2. Conquer : 나눠진 문제가 여전히 분할이 가능하면, 또 Divide를 수행하고, 그렇지 않으면 문제를 푼다.
    • 문제의 크기를 최대로 줄이게 되면 바로 답을 구할 수준이 됨, 이게 재귀 함수를 이용해서 문제를 풀때의 기저 사례와 같음, 그래서 분할 정복은 재귀 호출과 궁합이 잘 맞음
  3. Combine : Conquer 한 문제들을 통합해서 원래 문제의 답을 얻는다.

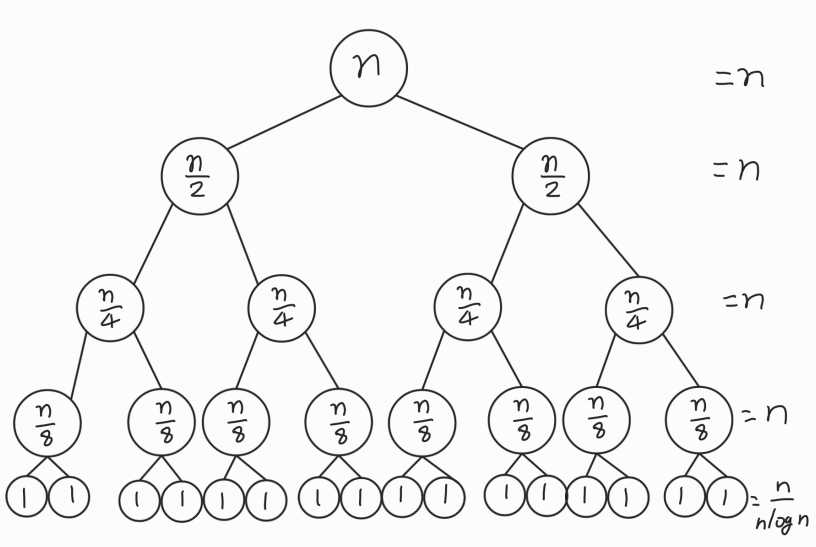
분할정복4

위 그래프가 분할정복 알고리즘의 대략적인 모습이다. 가장 많이 볼 수 있는 문제인 집합을 2개의 절반 크기로 분할하는 경우를 통해 시간복잡도를 이해해보자

문제의 크기(데이터 집합의 크기)를 N이라고 할 때, 한 단계 분할했을 때의 크기는 N/2가 된다. 기저 사례가 N=1인 문제라면 몇 번 분할될까? log₂N 번이다. N이 2의 거듭제곱인 경우에는 정확히 log₂N 번이고 아닐 때는 조금 더 많이 분할 될 수 있지만 많아 봐야 N*2일때를 넘지 못한다. 2^(k-1) < N <= 2^k일때 k번 분할되게 된다. 분할된 단계의 경우를 O(logN)으로 표현할 수 있다. 그리고 각 단계에 따라 분할되는 집합의 개수는 단계를 0, 1,.. k라고 봤을 때 2^k개이다.

정리하자면 문제의 크기를 N이라고 하고 현재 단계를 k라고 할 때 각 단계의 부분집합의 크기 : 2^k, 분할 후 문제의 크기 : N/(2^k), 각 문제마다 병합(conquer) 단계에서 걸리는 시간 : O(N) K 단계일때 병합할 때 걸리는 시간 : O(N/(2^K))이다.

각 문제마다 병합단계에서 걸리는 시간이 왜 O(N)인지는 병합 정렬 설명을 하면서 하겠다.

그럼 단계별 병합을 할 때 걸리는 시간은

0단계: 1 * O(N) 1단계: 2 * O(N/2) 2단계: 4 * O(N/4) … K단계: 2^K * O(N/(2^K)) = O(N)

각 단계마다 부분집합의 크기 역시 지수적으로 줄어드는 만큼 증가하고 있기 때문에 일반화하면 각 단계의 시간복잡도는 O(N)이다.

아까 위에서 구했듯이 분할된 단계의 개수는 총 O(logN)개 이므로 두개를 곱하면 O(NlogN)이라는 시간복잡도를 구할수 있다.

대표적인 예시

  1. 병합정렬 (merge sort)
  2. 이분탐색 (binary search)
  3. 거듭제곱 연산 (a^b)
  4. 피보나치 수열

예시 중에 병합정렬을 더 자세히 보여주겠다. (이분탐색은 따로 다룰 예정)

병합정렬(Merge Sort)

시간복잡도 : O(n log n) 공간복잡도 : O(n)

  1. 정렬한 데이터의 집합 크기가 0 or 1이 아니면(기저조건) 데이터의 집합을 반으로 divide 해준다.

  2. divide가 끝나면 같은 집합에서 나눠진 데이터들을 정렬하면서 병합하여 하나의 집합으로 만든다.
  3. 데이터 크기가 다시 원래대로 돌아올때까지 2를 반복

ex)

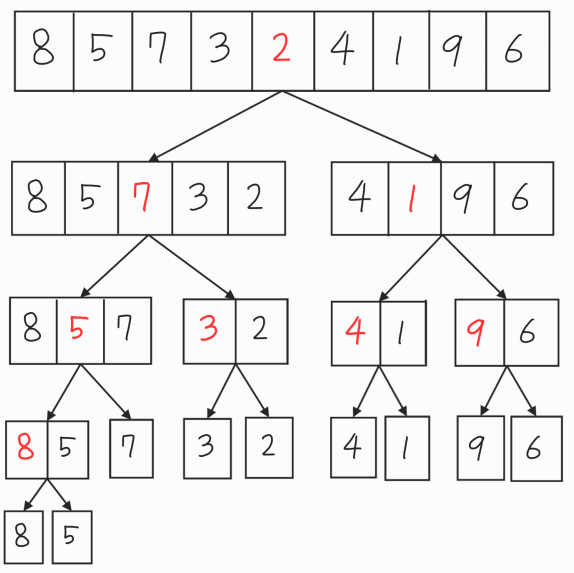
다음과 같은 데이터 집합이 있다.

분할정복1

1번의 과정을 하여 나눠준다.

분할정복2

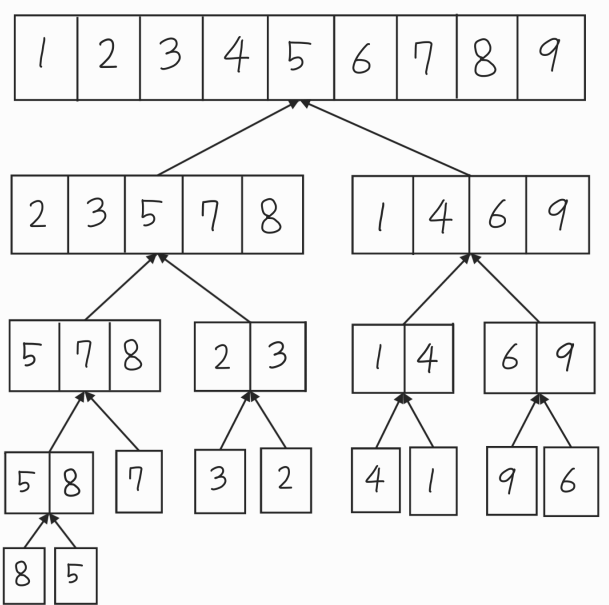
분할이 다 끝나면 2,3 번 과정을 반복해준다.

분할정복3

조각난 데이터를 정렬해가면서 병합하면 하나의 정렬된 데이터 집합을 얻을수 있게 된다.

여기서 병합하면서 어떻게 정렬하고 각 문제마다 병합(conqure) 단계에서 걸리는 시간복잡도가 O(N)인 이유를 알아보자.

두 데이터 집합을 정렬하면서 합치는 법

  1. 두 데이터 집합의 크기 만큼의 크기를 가지는 빈 데이터 집합을 만든다.
  2. 두 데이터 집합의 첫 번째 요소들을 비교하여 작은 요소를 빈 데이터 집합에 추가한다. 그리고 새 데이터 집합에 추가한 요소는 원래 데이터 집합에서 삭제한다.
  3. 원래 두 데이터의 집합 요소가 모두 삭제 될때 까지 2를 반복한다.

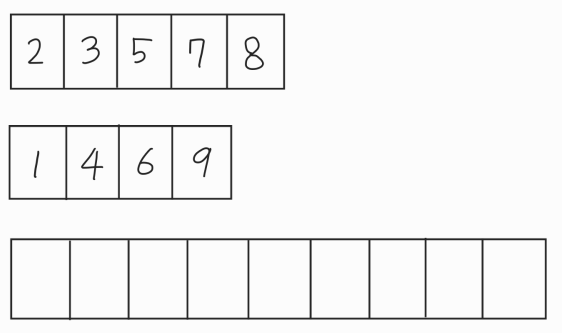
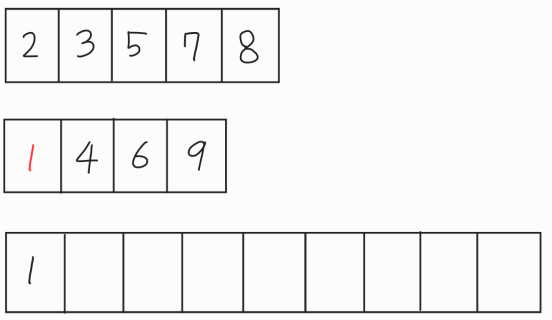
ex) 위의 두번째 단계를 가져와봤다. 두 단계의 합만큼의 크기를 가진 빈 데이터가 있다고 가정하자.

분할정복5

두 데이터의 집합의 첫번째 요소를 비교해서 더 작은 값을 빈 데이터에 삽입하고 삽입한 값은 원래의 데이터 집합에서 삭제한다. 예시에서는 첫번째 집합의 2와 두번째 집합의 1을 비교해서 1이 더 작으므로 빈 데이터에 넣어준다.

분할정복6

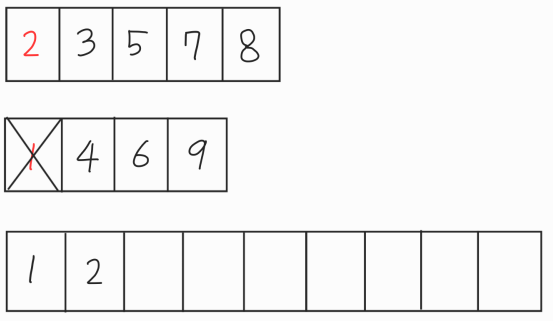
1을 삭제하고 2와 4를 비교한 후 더 작은 2를 빈 데이터에 넣어준다.

분할정복7

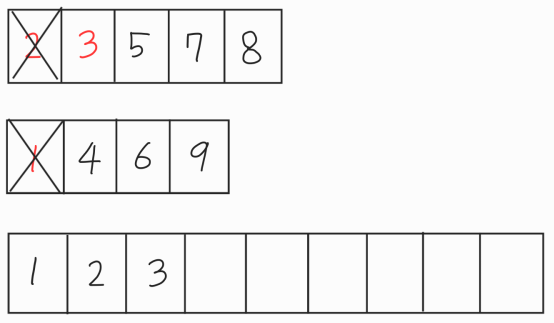
마찬가지로 2를 삭제하고 3과 4를 비교한 후에 더 작은 3을 넣어준다.

분할정복8

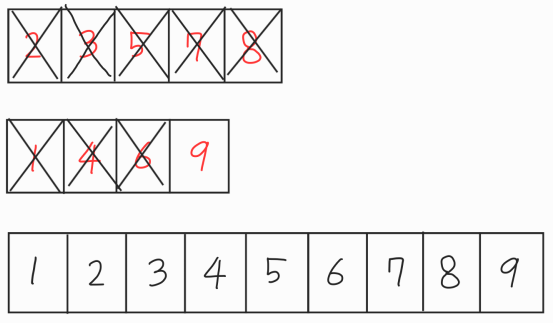
이런 과정을 반복하면 두 데이터는 전부 삭제되고 비어있던 데이터 집합은 정렬된 데이터 집합이 되었다.

분할정복9

단순히 첫 번째 데이터를 비교하는 시간과 삭제하는시간복잡도는 O(1)이므로, 병합하고 정렬하는 과정은 O(병합해야할 두 데이터의 크기의 합)이라는 시간복잡도를 가지게 된다. 그러므로 각 문제마다 병합단계에서 걸리는 시간 복잡도는 O(N)이 되고 아까 증명했듯이 전체 시간복잡도는 O(NlogN)이다.

버블 정렬, 선택 정렬 등의 기본적인 알고리즘이 O(N^2)이라는 점에서 보면 굉장한 발전이라고 할 수 있다. 현재 일반적인 알고리즘 중 가장 빠른 퀵 정렬 또한 분할 정복 기법을 사용한다.

C++의 STL에 속한 sort 함수, C의 qsort 함수 등 여러 언어의 라이브러리에서 이 빠른 분할 정복을 베이스로 한 정렬 함수를 지원한다.

관련 문제

Comments

You May Also Enjoy