Hong

끄적끄적

6. 깊이 우선 탐색(dfs)

dfs 대해 알아보기 전에 그래프에 대한 기초가 필요하다. https://hong1995.github.io/stl/Graph/ 를 참고 하자.

깊이 우선 탐색(dfs)

DFS(Depth First Search) 이름 뜻 그대로 루트 노드나 임의의 노드에서 시작하여 최대로 진입할 수 있는 깊이까지 탐색하고 다시 돌아와 다른 노드로 같은 방식으로 탐색하는 방법을 말한다.

장점

  • 최선의 경우, 가장 빠른 알고리즘이다. 운이 좋게 항상 해에 도달하는 올바를 경로를 선택하다면, dfs가 최소 실행시간에 해를 찾는다.
  • bfs에 비해 저장공간의 필요성이 적다. 백트레킹을 해야하는 노드들만 저장해주면 된다.

단점

  • 찾은 해가 최적이 아닐 가능성이 있다.(알고리즘은 항상 최악의경우를 생각해야함)
  • 최악의 경우, 가능한 모든 경로를 탐험하고서야 해를 찾으므로, 해에 돨하는데 가장 오랜 시간이 걸린다.

예를 들어보자!!

dfs1

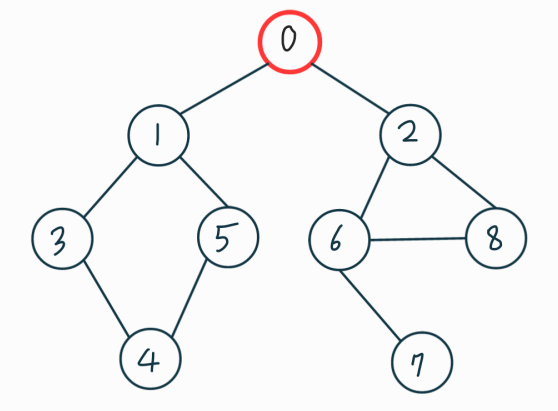
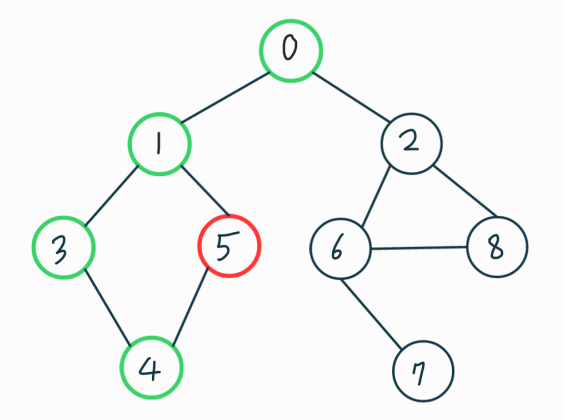
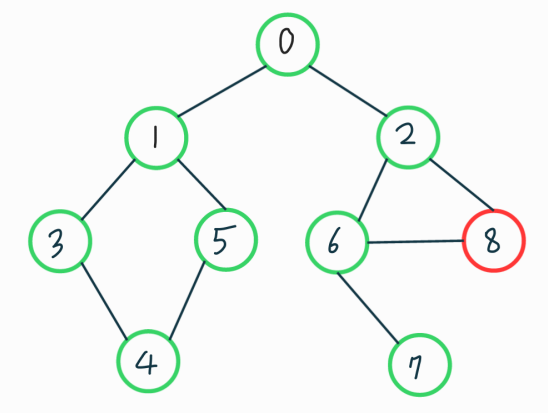
먼저 정점을 하나 선택한다. 선택된 정점의 인접란 정점중에 아직 방문하지 안은 정점 중 하나를 선택해 방문한다. 위에서 설명 했듯이 깊이 우선 탐색이므로 0에 인접한 1에 방문 하였다면 그 다음엔 1에 인접한 정점들이 우선적으로 탐색 되게 된다. 그래프를 보면서 알아보자. 빨간색은 현재 방문한 노드이고 초록색은 방문했던 노드입니다.

dfs2

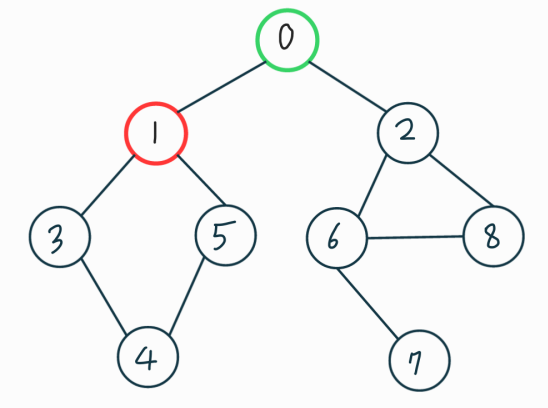
맨 처음 방문한 0번 노드의 인접한 노드는 1, 2 번이다. 이중에서 더 작은 번호의 1번노드를 방문했다(인접 리스트에 저장된 순서대로 방문). 이 다음에는 2번이 아니라 1번에 인접하고 있는 0, 3, 5번 노드중 하나를 방문할 건데, 0은 이미 방문을 했으므로 3, 5번 중에 방문하게 된다.

dfs3

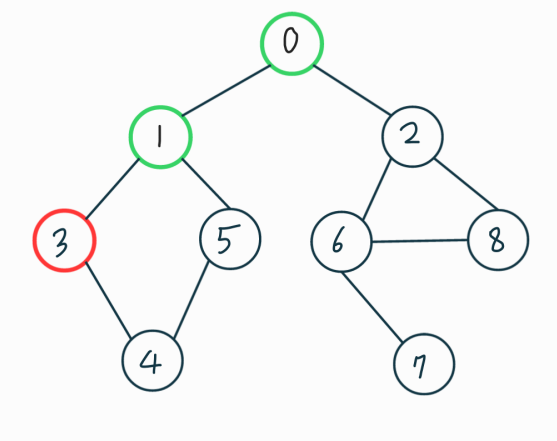
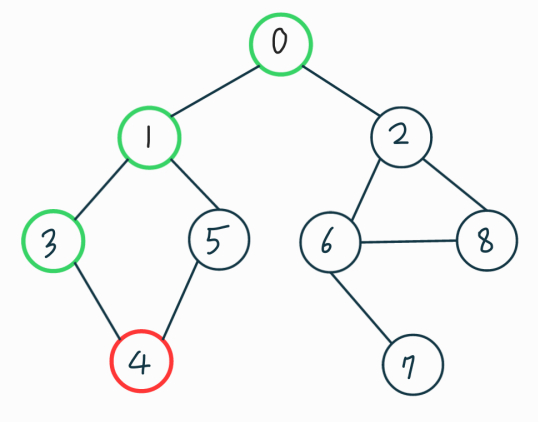
더 작은 번호인 3을 방문하였다. 마찬가지로 3번에 인접한 노드는 1, 4 이고 1은 방문했었으므로 4를 방문 할것이다.

dfs4

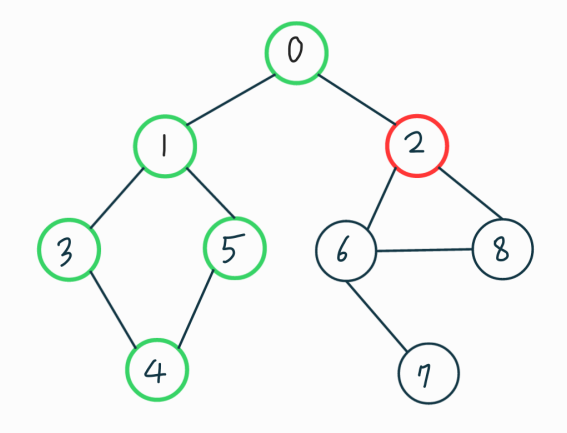
5번노드를 방문할수 밖에 없다.

dfs5

5번 노드에선 더 이상 방문하지 않은 인접한 노드가 없다. 그러면 4번 노드로 돌아가서 4번 노드의 이접한 노드들 중 아직 방문하지 않은 정점을 찾아 방문해야 한다. 4번에도 없으면 3번, 없으면 1번…이렇게 확인하면서 돌아가서 0번 노드까지 오게된다.

dfs6

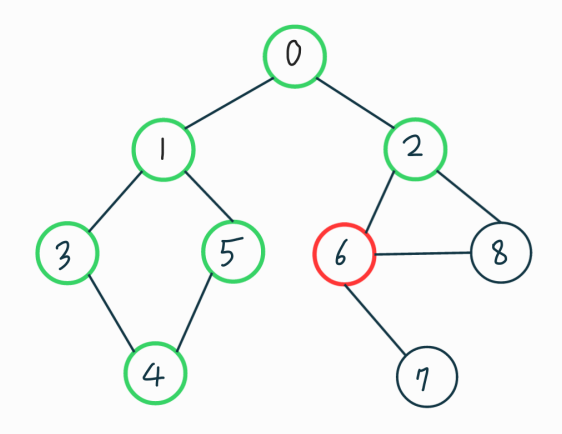
0번노드에 인접한 노드들 중에 아직 방문하지 않은 2번 노드가 있으므로 방문한다.

dfs7

똑같은 방식으로 진행한다.

dfs8

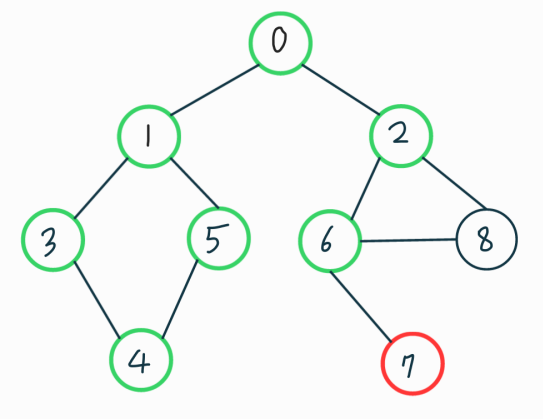
마찬가지..

dfs9

8번 노드를 방문하게 되면 아무리 다시 돌아가도 더 이상 방문할 노드가 남지 않게 된다. 그래프 전체를 탐색한것이다.

어떠한 정점에서 더 이상 방문할 노드가 없을 꺠 자신을 불렀던 정점으로 되돌아가는 것은 어떻게 구현을 할수 있을까. 두가지 방법이 있다.

첫번째는 스택이다. https://hong1995.github.io/stl/Stack/ 방문하는 순서대로 노드를 스택에 쌓고, 방문이 끝나면 스택에서 pop해주고 꼭대기값에 인접한 방문하지 않은 노드가 있는지 확인하는 방식으로 구현이 가능하다.

두번째는 재귀함수이다. 재귀함수 또한 스택 메모리 동간에 쌓아 올려지는 구조를 띄기 때문에 재귀함수를 사용해도 이것을 구련할수 있다. 주로 이 방법을 사용한다. 코드를 통해서 보자.

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
bool visited[10]; // 노드 방문시 방문 여부를 검사하기위한 배열
vetor<int> adj[10]; // 인접리스트(벡터)를 이용해서 그래프 만들기
void dfs(int now){
	visited[now]=1;
	for(nt i=0; i<adj[now].size(); i++){
		int next = adj[now][i];
		if(!visited[next])dfs(next);
	}
}

dfs의 시간 복잡도

O(V+E)

정점과 간선의 개수 합이다. 한 번 방문한 노드는 다시 방문하지 않으며, 한 노드에서 다음으로 방문할 노드들을 순회하는 횟수가 그 노드의 차수와 같기 떄문이다.

만약 인접 리스트가 아니라 인접 행렬로 그래프를 구성하게 된다면 다음에 방문할 정점을 찾을 때 모든 정점을 순회하며 둘이 이어져 있는지를 체크해야 하므로 O(V^2)이다. 경우에따라서 시간차이가 크게 나게 된다.

관련문제

Comments

You May Also Enjoy