Hong

끄적끄적

분할정복의 종류 중에 이분탐색을 자세히 다뤄보자.
N개의 정렬되어 있는 수들 중 어떤 값 K의 위치를 탐색범위를 두 부분으로 분할해서 찾는 방식이다. 그냥 순서대로 탐색하게 되면 O(n)이지만 이분탐색을 사용하게 되면 O(logn)의 시간복잡도를 보여준다.

어떻게 사용하는가?

  1. 이분 탐색을 하고자 할 때 이미 정렬이 되어있어야 한다.
  2. 양쪽 끝값을 left, right로 가운데 값을 mid로 잡아준다.
  3. mid 값과 구하고자 하는 값을 비교 한다.
  4. 비교할시 mid 값보다 구하고자 하는 값이 크면 left를 mid+1로 만들어주고 낮으면 right를 mid-1로 만들어 준다
  5. left >= right 가 될때까지 반복해서 구하고자 하는 값을 찾는다.

예시

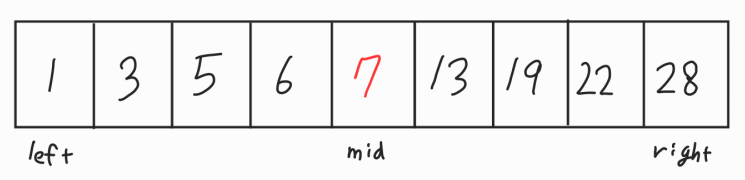
N = 9인 정렬된 배열에서 6을 찾아보자. 맨 왼쪽인 1을 left 맨 오른쪽인 28을 right 가운데 7을 mid로 잡는다.

이분탐색1

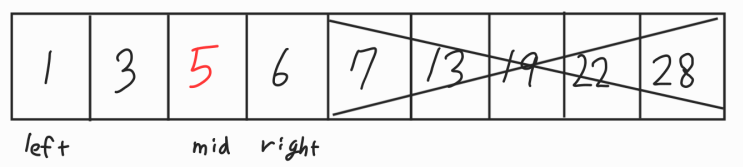
mid값이랑 6을 비교했을때 찾고자하는 값이 더 작으므로 더이상 mid값을 포함해서 오른쪽은 탐색할 필요가 없다. right값을 mid-1로 바꾼다.

이분탐색2

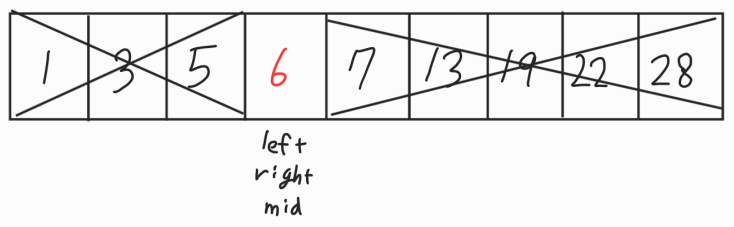
마찬가지로 mid값 5와 6을 비교해서 mid가 더 작으므로 이번에는 left를 mid+1로 바꾼다.

이분탐색3

남은 값이 6밖에 없으므로 바로 찾을수가 있다.

이분탐색은 일반적인 분할정복처럼 병합의 과정이 없다. 한 수만 찾는 것이기 떄문에 분할을 해서 그중 한 문제만 풀기 떄문이다. 분할정복에서 병합의 O(n)시간이 빠지기 때문에 시간복잡도는 O(logn)이 된다.

코드

위 그림에서 이분탐색으로 수를 찾는 코드를 간단하게 짜보았다.

#include <iostream>
using namespace std;
int f=0,result = 0;
int arr[10] = { 1, 3, 5, 6, 7, 13, 19, 22, 28 };
int main() {
	cin >> f;//찾는수
	int left = 0, right = 8;
	while (left <= right) {
		int mid = (left + right) / 2;
		if (arr[mid] > f)
			right = mid - 1;
		else if (arr[mid] < f)
			left = mid + 1;
		else{
			result = mid;
			break;
		}
	}
	cout << result << "\n";
	return 0;
}

관련문제

Comments

You May Also Enjoy