Hong

끄적끄적

7. 너비 우선 탐색(bfs)

bfs 대해 알아보기 전에 그래프에 대한 기초가 필요하다. https://hong1995.github.io/stl/Graph/ 를 참고 하자.

너비 우선 탐색(bfs)

BFS(Breadth First Search) 이름 뜻 그대로 임의의 정점에서 시작해서 인접한 정점을 먼저 탐색하는 방법으로, 시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법입니다.

장점

  • 너비를 우선으로 탐색하기 때문에 답이 되는 경로가 여러 개인 경우에도 최단 경로임을 뽀장
  • 최단 경로가 존재한다면, 어느 한 경로가 무한히 깊어진다 해도 최단 경로를 반드시 찾을 수 있다.
  • 노드 수가 적고 깊이가 얕은 해가 존재 할 때 유리하다.

단점

  • 재귀호출을 사용하는 DFS와 달리 큐를 이용해 다음에 탐색 할 노드들을 저장하기 때문에 노드의 수가 많을 수록 필요없는 노드들까지 저장해야 하기 때문에 더 큰 저장공간 필요.
  • 노드의 수가 늘어나면 탐색해야하는 노드가 많아지기 때문에 비효율적

큐를 이용해서 구현한다.

https://hong1995.github.io/stl/Queue/

  1. 탐색 시작 노드를 큐에 삽입하고 방문했는지 체크해준다
  2. 큐에서 top노드를 꺼낸 뒤에 해당 노드의 인접 노드 중 방문하지 않은 노드를 모두 큐에 삽입 후 방문했는지 체크 해준다.
  3. 2번 반복

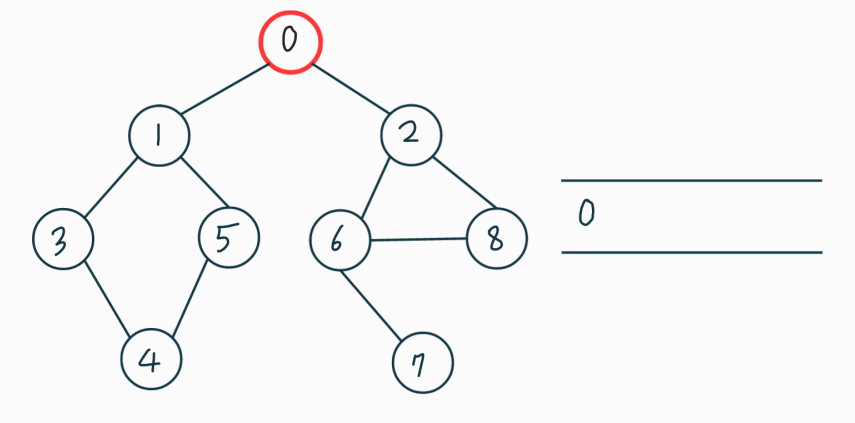
image-20220223003016000

맨 처음 0번 정점부터 방문을 시작한다.
0을 큐에 집어넣는다.

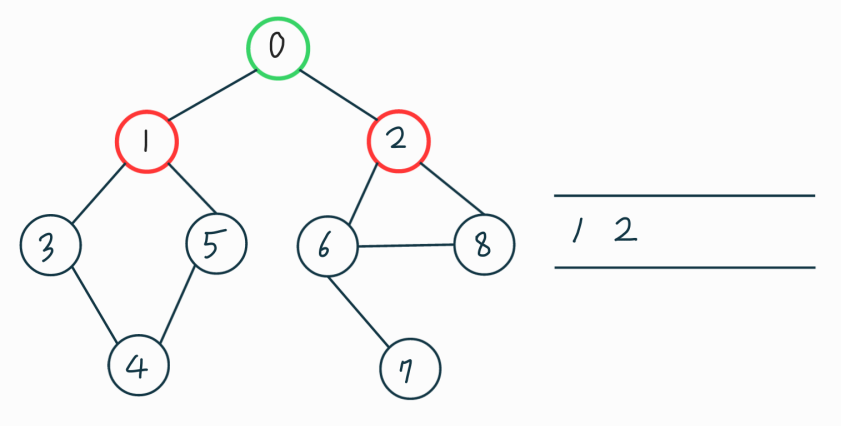
image-20220223003040575

0을 큐에서 pop해주고 0과 인접하고 방문하지 않은 점을 큐에 push 해준다.

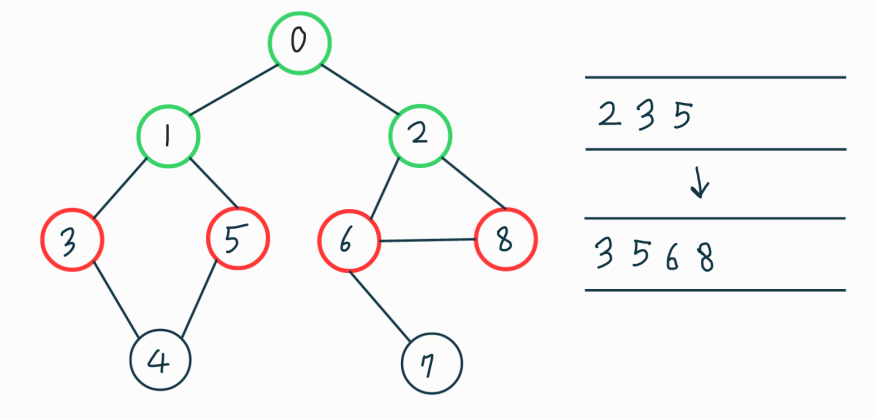
image-20220223003059206

큐에서 top에 있는 1을 pop해주고 3, 5를 push 해줍니다.
그리고 top에 있는 2를 pop해주고 6, 8을 push 해줍니다.

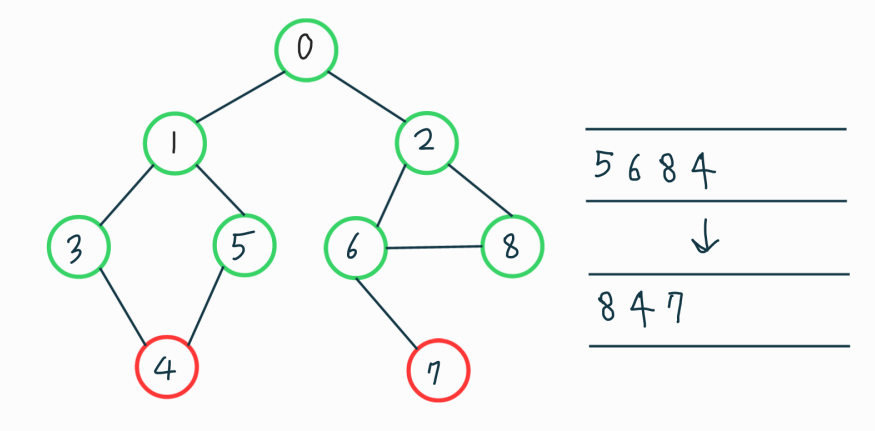
image-20220223003119295

같은 과정.. 큐에서 pop되는 순서대로 탐색하면 bfs가 잘 동작하는걸 확인 할수 있다.

여기서 0번 노드, 즉 시작점을 방문한 것을 0단계라 하고 그 다음 그림부터 1, 2, 3단계라고 부를 때 각 단계의 정점들은 그 안에서 방문 순서가 바뀔 수는 있지만, 다른 단계와는 방문 순서가 절대 뒤섞이지 않는다. 그러므로 각 간선의 비용이 전부 1로 같다고 생각하면 K단계에 방문하는 정점들은 시작점으로 부터 최소비용이 K이다.

특정 조건의 최단 경로 알고리즘을 계산할 때 사용하는 경우가 많다.

코드

#include<iostream>
#include<vector>
#include<queue>
#include<algorithm>
using namespace std;
bool visited[10];
vector<int>adj[10];
queue<int>q;
void bfs(int st){
    visited[st]=1;
    q.push(st);
    while(!q.empty()){
        int now = q.front();
        q.pop();
        for(int i=0; i<adj[now].size(); i++){
            int next = adj[now][i];
            if(!visited[next]){
                visited[next]=1;
                q.push(next);
            }
        }
    }
}

bfs의 시간복잡도

O(V+E)

BFS도 DFS와 마찬가지로, 인접 리스트를 사용하였을 때의 시간 복잡도는 정점과 간선의 갯수의 합인 O(V+E)이다.

관련 문제

Comments

You May Also Enjoy